नमस्कार दोस्तों आज की इस पोस्ट में हम प्राकृतिक संख्या की समस्त जानकारी पढ़ने वाले हैं तो पोस्ट को पूरा जरूर पढ़िए। चलिए प्राकृतिक संख्या की जानकारी पढ़ना शुरू करते हैं।
प्राकृतिक संख्या किसे कहते हैं
गिनती में उपयोग की जाने वाली सभी संख्याएं प्राकृतिक संख्या कहलाती हैं।
जैसे :-1, 2, 3, 4, 5, 6, 7, 8, 9………
प्राकृतिक संख्या को N से प्रदर्शित करते हैं।
प्राकृतिक संख्या को अंग्रेजी में "Natural Number" कहते हैं।
जिन संख्याओं को किसी वस्तु के गिनने के काम में लिया जाता हैं उन्हें प्राकृतिक संख्याएँ कहते है।
जैसे :-
- बस्ते में 5 किताबें रखी हैं।
- टेबल पर 4 पेन रखे हैं।
- गणित की कक्षा में 30 छात्र पढ़ते हैं।
प्राकृतिक संख्या का उपयोग क्रम में रखने के लिए भी किया जाता हैं।
जैसे:-
- राम ने कक्षा 10वीं में पहला स्थान पाया।
- सीता ने Law में 4वां स्थान प्राप्त किया।
- श्यामू कक्षा में छटवें स्थान पर बैठता हैं।
प्राकृतिक संख्याओं के सूत्र
- प्रथम n प्राकृतिक विषम संख्याओं का औसत = n
- प्रथम n प्राकृतिक सम संख्याओं का औसत = n + 1
- प्राकृतिक संख्याओं का योग = (पहली संख्या + अंतिम संख्या / 2) × n
- प्रथम n प्राकृत संख्याओं का औसत = ( n + 1 ) / 2
- लगातार n तक विषम प्राकृत संख्याओं का औसत = (n + 1) / 2
- लगातार n तक विषम प्राकृत संख्या का योग = (n/2 + 1)
- N = (अंतिम संख्या – पहली संख्या / वर्ग अंतराल) +1
- प्रथम n प्राकृत संख्याओं के वर्गों का योग = n( n + 1 )( 2n + 1 ) / 6
- प्रथम n प्राकृत संख्याओं के घनों का योग = [ n (n + 1) / 2 ]²
महत्वपूर्ण बिंदु :
- सबसे छोटी प्राकृतिक संख्या 1 होती हैं।
- सबसे बड़ी प्राकृत संख्या अनन्त हैं।
- समुच्च में 0 को प्राकृतिक संख्या माना जाता है।
- प्राकृतिक संख्या संख्या पद्धति का एक भाग हैं।
- प्राकृतिक संख्या को N द्वारा प्रदर्शित किया जाता है।
- प्राकृतिक संख्याओं को प्राचीन इतिहास के आधार पर हिन्दी अरबी संख्या कहाँ जाता हैं।
- प्राकृत संख्या में 1 इकाई की लगातार बढ़ोतरी होती रहती है।
- प्राकृत संख्या = 0 < N ≤ 1 होता हैं।
- समुच्चय में N0 = {1, 2, 3, 4, 5, 6, 7, 8, 9, ……) द्वारा सूचित किया जाता है।
प्रथम 10 प्राकृतिक संख्याओं का योग
प्रथम 10 प्राकृतिक संख्या = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
प्रथम 10 प्राकृतिक संख्याओं का योग = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
प्रथम 10 प्राकृतिक संख्याओं का योग = 55
अतः प्रथम 10 प्राकृतिक संख्याओं का योग 55 होता हैं।
प्रथम 10 प्राकृत संख्याओं के वर्गों का औसत कितना है?
वर्ग (Square) की परिभाषा : जब किसी संख्या को उसी संख्या से गुणा किया जाता हैं तो प्राप्त गुणनफल को संख्या का वर्ग कहते हैं।
1 से 10 तक का वर्ग
| 1 का वर्ग | 1 |
| 2 का वर्ग | 4 |
| 3 का वर्ग | 9 |
| 4 का वर्ग | 16 |
| 5 का वर्ग | 25 |
| 6 का वर्ग | 36 |
| 7 का वर्ग | 49 |
| 8 का वर्ग | 64 |
| 9 का वर्ग | 81 |
| 10 का वर्ग | 100 |
प्रथम 10 प्राकृत संख्याओं के वर्गों का योग = 1 +4 + 9 + 16 + 25 + 36 + 49 + 64 + 81 + 100
प्रथम 10 प्राकृत संख्याओं के वर्गों का योग = 385
जरूर पढ़िए :
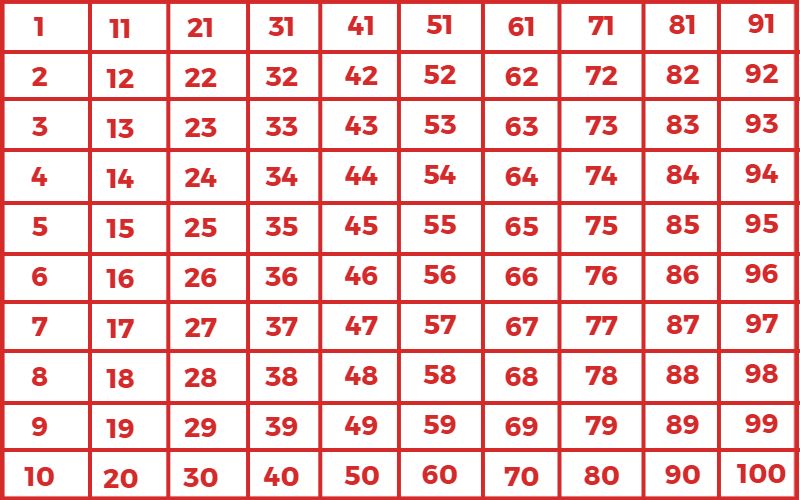
1 से 100 तक प्राकृतिक संख्या
प्राकृतिक संख्या पर आधारित प्रश्न
Q.1 1+2+3+4 ……………… 18+19+20 = ?
A. 120
B. 210
C. 240
D. 320
हल:- प्रश्नानुसार,
1+2+3+4 ……………… 18+19+20 = ?
अंतिम संख्या = 20
प्रथम संख्या = 1
N = (अंतिम संख्या – पहली संख्या)/वर्ग अंतराल + 1
N = ( 20 – 1 ) / 1 + 1
N = 19 + 1
N = 20
योग = ( पहली संख्या + अंतिम संख्या / 2 ) × n
योग = (1 + 20 ) / 2 ×20
योग = 21 × 20 / 2
योग = 21 × 10
योग = 210
Ans. 210
Q.2 1+2+3+4 ……………… 78+79+80 = ?
A. 1,220
B. 1,880
C. 3,240
D. 4,860
हल:- प्रश्नानुसार,
1+2+3+4 ……………… 78+79+80 = ?
अंतिम संख्या = 80
प्रथम संख्या = 1
N = (अंतिम संख्या – पहली संख्या)/वर्ग अंतराल + 1
N = ( 80 – 1 ) / 1 + 1
N = 79 + 1
N = 80
योग = ( पहली संख्या + अंतिम संख्या / 2 ) × n
योग = (1 + 80 ) / 2 × 80
योग = 81 × 80 / 2
योग = 81 × 40
योग = 3,240
Ans. 3,240
Q.3 1 से 49 तक कि सभी विषम संख्याओं का योग बताइए?
A. 360
B. 625
C. 720
D. 800
हल:- प्रश्नानुसार,
1 + 3 + …………….………+ 48 + 49
पहली संख्या = 1
अंतिम संख्या = 49
N = (अंतिम संख्या – पहली संख्या)/वर्ग अंतराल + 1
N = (49 – 1)/2 + 1
N = 48/2 + 1
N = 24 + 1
N = 25
प्राकृतिक संख्याओं का योग = (पहली संख्या + अंतिम संख्या)/2 × n
योग = (1 + 49)/2 × 25
योग = 50/2 × 25
योग = 25 × 25
योग = 625
Ans. 625
Q.4 1 से 20 तक की सभी प्राकृतिक संख्याओं के वर्गों का योग बताये?
A. 1,385
B. 4,350
C. 2,260
D. 2,870
हल:- प्रश्नानुसार,
n = 20
योग = n (n + 1) (2n + 1) / 6
योग = 20 (20 + 1) (2 × 20 + 1) / 6
योग = 20 × 21 (40 + 1) / 6
योग = (20 × 21 × 41) / 6
योग = 17,220 / 6
योग = 2,870
Ans. 2,870
Q.5 1 से 80 तक की सभी प्राकृतिक संख्याओं के वर्गों का योग बताये?
A. 1,37,895
B. 1,24,350
C. 2,26,670
D. 1,73,880
हल:- प्रश्नानुसार,
n = 80
योग = n (n + 1) (2n + 1) / 6
योग = 80 (80 + 1) (2 × 80 + 1) / 6
योग = 80 × 81 (160 + 1) / 6
योग = (80 × 81 × 161) / 6
योग = 1,043,280 / 6
योग = 1,73,880
Ans. 1,73,880
Q.6 1 से 40 तक की सभी प्राकृतिक संख्याओं के घनों का योग क्या हैं?
A. 468,900
B. 672,400
C. 678,908
D. 566,902
हल:- प्रश्नानुसार,
[n (n + 1) / 2]²
n = 40
[40 (40 + 1) / 2]²
(40 × 41 / 2)²
(1,640 / 2)²
(820)²
Ans. 672,400
Q.7 किसी प्राकृत संख्या के वर्ग के तिगुने में से उस संख्या के चार गुने को घटाने पर प्राप्त संख्या उस संख्या से 50 अधिक हैं। वह संख्या हैं?
A. 4
B. 5
C. 6
D. 10
हल:- प्रश्नानुसार,
माना, प्राकृतिक संख्या x हैं।
तब, x² × 3 – 4x = x + 50
3x² – 4x – x = 50
3x² – 5x = 50
3x² – 5x – 50 = 0
3x² + 10x – 15x – 50 = 0
x (3x + 10) – 5 (3x + 10) = 0
(x – 5) (3x + 10) = 0
x – 5 = 0 , 3x + 10 = 0
x = 5 या 3x = – 10
x = 5 या x = – 10/3 (प्राकृतिक संख्या नहीं हैं।
Ans. x = 5 प्राकृतिक संख्या हैं।
Q.8 किसी प्राकृत संख्या के घन में से उसका वर्ग घटाने पर परिणाम 48 प्राप्त होता हैं। संख्या होगी?
हल:- प्रश्नानुसार,
माना, प्राकृतिक संख्या x हैं।
x³ – x² = 48
x² (x – 1) = 48
x² (x – 1) = 16 × 3
4² × (4 – 1)
x = 4
Q.9 किसी प्राकृत संख्या के घन से उसका वर्ग घटाने पर 100 प्राप्त होता हैं। वह संख्या हैं?
हल:- प्रश्नानुसार,
माना, प्राकृतिक संख्या x हैं।
x³ – x² = 100
x² (x – 1) = 100
x² (x – 1) = 25 × 4
5² × (5 – 1)
x = 5
Q.10 1 से 100 तक की सभी प्राकृतिक संख्याओं के घनों का योग क्या हैं?
A. 12,867,900
B. 18,234,400
C. 27,856,908
D. 25,502,500
हल:- प्रश्नानुसार,
[n (n + 1) / 2]²
n = 100
[100 (100 + 1) / 2]²
[(100 × 101) / 2]²
(10,100 / 2)²
(5,050)²
Ans. 25,502,500



You must be logged in to post a comment.